Video Transcript In this problem, we have to show that the tangent lines for the parabola X Square is equals toe four p y, drawn from any point on their direct tricks are perpendicular Now The equation off the ancient lines to the parable Expert examples toe four p y at point x not Why not is given by Ex Medical X, nor is equals toe p 9 26 Locate The Centroid X Of The Shaded Area Y 1 4x 2 Youtube Consider the parabola y=x^2 the shaded area is (1 1) Consider the parabola y=x^2 the shaded area is (1 1) Consider the parabola y=x^2 The shaded area is Get the answers you need, now!In the graph given below, the equation of the parabola is x = (y2) 2 /2 and the equation of the(x0) 2 (yp) 2 = (yp) 2 (xx) 2 x 2 (yp) 2 = (yp) 2 If we expand all the terms and simplify, we obtain x 2 = 4py Although we implied that p was positive in deriving the formula, things work exactly the same if p were negative That is if the focus lies on the negative y axis and the directrix lies above the x axis the equation of the
705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino
Centroid of parabola y=x^2
Centroid of parabola y=x^2-Centroid for Cshapes John Ray Cuevas Area 1 x = 6000 millimeters y = 00 millimeters Area 2 x = millimeters y = 6500 millimeters Area 3 x = 60 millimeters y = 110 millimeters d Solve for the Ax values Multiply the area of each region by the distances from the yaxisThis engineering statics tutorial goes over how to find the centroid of the area under a parabola It requires a simple integrationIf you found this video h



Area By Integration Mathalino Reviewers ged With Area By Integration
Find the centroid of the region bounded by y = 4 x^2 and the xaxis Question Find the centroid of the region bounded by y = 4 x^2 and the xaxis This problem has been solved! Centroid nth Degree Parabola (convex) This equation computes the x and y components of the Centroid for an nth degree parabola, convex up, where the equation for the parabola is y = ( h b1 n)x1 n ( h b 1 n) x 1 n The Centroid ( C) represents center of mass of the parabola The Centroid has x & y units of length representing a coordinateFirst week only $499!
2 > @ y > a x dx@ yA y dA a x dx a x •Evaluate the centroid coordinates 3 4 ab a 2b x xA Q y x a 4 3 3 10 ab ab 2 y yA Q x y b 10 3 5 22 Theorems of PappusGuldinus •Surface of revolution is generated by rotating a plane curve about a fixed axis •Area of a surface of revolution isFree Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experienceQuestion 2 Find the shortest distance between the line y – x = 1 and the curve x = y 2 (1/4, 1/2) is point on a parabola Question 3 Two common tangents to the circle x 2 y 2 = 2a 2 and parabola y 2 = 8ax are Solution Let y = mx 2a/m be equation of tangent to any parabola y 2
X y L 2 wx 0 38 Centroids by Integration Riemann Sums 39 Centroids by Integration Wednesday, Wednesday, Centroids from Functions !Centroid x Added by htmlvb in Mathematics Calculates the x value of the centroid of an area between two curves in bounds a, b Centroids Reference Table This page references the formulas for finding the centroid of several common 2D shapes In the figures, the centroid is marked as point C Its position can be determined through the two coordinates x c and y c , in respect to the displayed, in every case, Cartesian system of axes x,y



Find The Coordinates Of The Centroid Of A Triangle With Vertices




Determine The Centroid X Y Of The Shaded Area Youtube
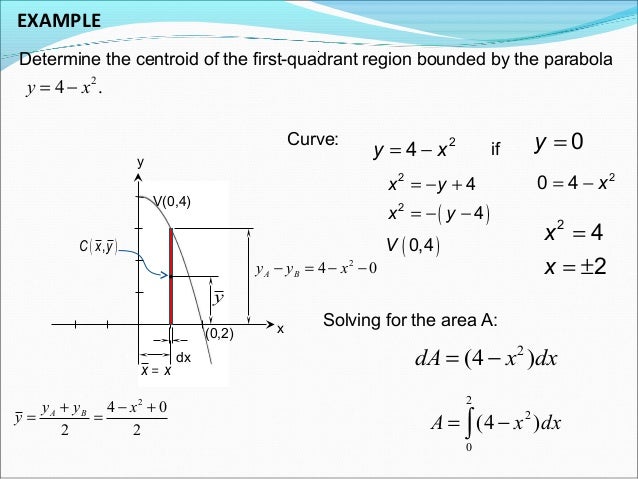
For the height of the centroid, you need to find the moment of the paraboloid about the $x$$y$ plane The crosssectional area at height $z$ is $\pi(x^2y^2)=\pi z$ A thin slice of thickness $dz$ at that height has approximate volume $\pi z\,dz$, and therefore moment about the $x$$y$ plane approximately $z(\pi z \,dz)$Answer to Find the centroid of the area bounded by the parabola y =4x^2 and the xaxis?Determine the centroid of the first quadrant region bounded by the parabola y=4x^2 close Start your trial now!
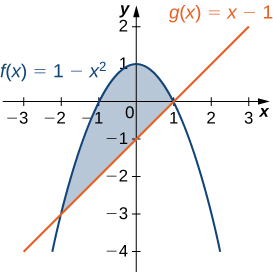



6 6 Moments And Centers Of Mass Calculus Volume 1



5 Centroid Of An Area By Integration
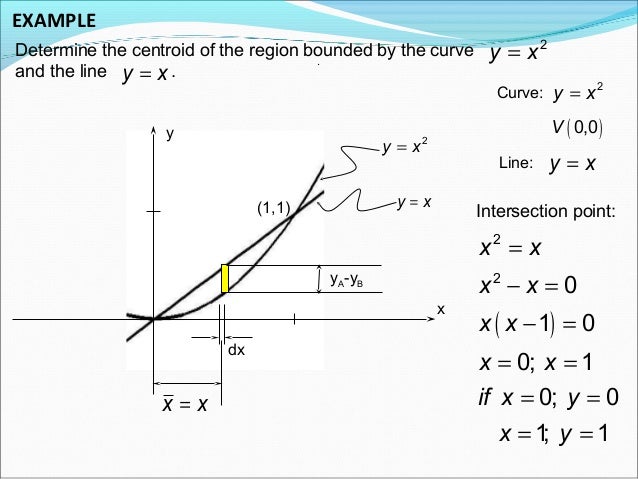
Solution Find the coordinates of the centroid of the plane area bounded by the parabola and xaxis Solution Locate the centroid of the plane area bounded by y = x^2 and y = x Solution Find the area of the curve r^2 = a^2 cos 2θ The equations of the parabolas are The centroid of the region has coordinates It can be found using , where is the coordinates of the centroid of the differential element of area dA Use differential elements consisting of rectangular vertical slices of width dx and height yThis means that variable x will be the variable of integration In this case, and Locate the centroid of the plane area bounded by the equation y^2 = 4x, x = 1 and the xaxis on the first quadrant Problem Answer The coordinates of the center of the plane area bounded by the parabola, the line and the xaxis of the first quadrant is at (3/5, 3/4)



Centroid Moment Of Inertia




1 Find The Mass And Centroid Of The Region Bounded By The Y2 With P Homeworklib
If ρ1 and ρ2 be the radii of curvature at the ends of a focal chord of the parabola y^2 = 4ax, then show that ρ1^–2/3 ρ2^–2/3 = (2a)^–2/3 asked in Mathematics by KumarManish ( 577k points)Let a circle tangent to the directrix of a parabola \{{y}^{2}}=2ax\ has its centre coinciding with the focus of the parabola Then the point of intersection of the parabola This equation computes the x and y components of the Centroid for an nth degree parabola, concave up, where the equation for the parabola is y = ( h bn)xn ( h b n) x n The Centroid represents center of mass of the parabola The Centroid has x& y units of length representing a coordinate




How To Find The Centroid Of The Area Under A Parabola Youtube



1
Answer This curve intersects the xaxis in the first quadrant at x=2 and the yaxis at y=4 So we need to find the area from x=0 to x=2 and find a point (P, Q) so that the area under the curve between 0 and P is equal to the area between P and 2, andArrow_forward Question Determine the centroid of the first quadrant region bounded by the parabola y=4x^2 * The parabola \\(y=x^2\\\) has three points \\(P\_1,P\_2,P\_3\\\) on it The lines tangent to the parabola at \\(P\_1, P\_2, P\_3\\\) intersect each other pairwise at




Centroids Centre Of Mass Centres Of Gravity



2
ybar = 1/A ∫ 1/2f(x) 2g(x) 2dx The Attempt at a Solution I know that the graph is a sideway parabola with vertex at (5,0) and bounded at x=0, this means that the graph is symmetrical above and below the xaxis so y value of centroid is 0 For the x value of the centroidThis clip shows how to fund the vertical centroid of both a parabola and a semicircle I show stepbystep how to set up the problem and how to solve itFind the area of the region bounded by the parabola y^2= 16x and its latus rectum Calculus Centers of Mass Find the centroid of the region in the first quadrant bounded by the xaxis, the parabola y^2 = 2x, and the line x y = 4 I've graphed the function, and it looks like a triangle with one side curved (the parabola)



2




Answered 5 Locate The Coordinates Of The Bartleby
2 x y= 2 8x y= −Determine the centroid of the area bounded by the parabolas and 2 x y= ( )0,0V Curve 1 dy y x (x1,y) (x2,y) (4,2) 2 x y= 2 8x y= − 2 1x x− x ( ),C x y y Curve 2 2 8x y= − ( )0,0V Solving for intersection points ( ) ( ) 2 2 4 4 3 8 8 8 0 8 0 0;Get an answer for 'Find the centroid of the area bounded byx^2=4y ;Answer (1 of 4) How do you find the centre of gravity of the section of the parabola y=x^2 between y=100 and y= using integration?



Lesson 12 Centroid Of An Area




Solved Find The Abscissa Of The Centroid Of The Region Between The Parabola Y 5 Aˆ X 2 And The Line Y 3 Aˆ 2x From X 0 To X 2
Y^2=4x (Area) Please show a graph or illustration and explain thoroughlyThank you enotes "NEED BADLY"' and find homeworkSee the answer See the answer See the answer done loading Show transcribed image text Expert Answer Find the centroid (¯ x, ¯ y) of the region bounded by y = 6x^27x, y = 0, x = 0, and x = 7 Calculus Find the dimensions of the rectangle of largest area that has its base on the xaxis and its other two vertices above the xaxis and lying on the parabola y=4−x^2




9 26 Locate The Centroid X Of The Shaded Area Y 1 4x 2 Youtube



1
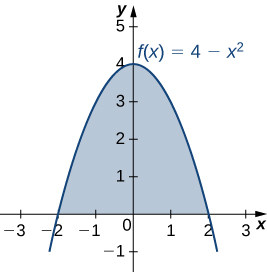
Answer and Explanation 1 y(x) = 4−x2 {Parabola with center at (0,4) This parabola opens downwards} y = x2 {Positive slope line} 4−x2 = x2 Interception points between functions x2x−2We could generate a series of rectangles to lay over the curve x y L 2 wx 0 40 CentroidsSolution for ) Find the centroid of the first quadrant area bounded by the parabola y = x2 and the line y = x a (1/3, 3/4) %3D b (1/3, 3/4) c (1/2, 2/5)




First Moments And Centroids Mcgraw Hill Education Access Engineering



2
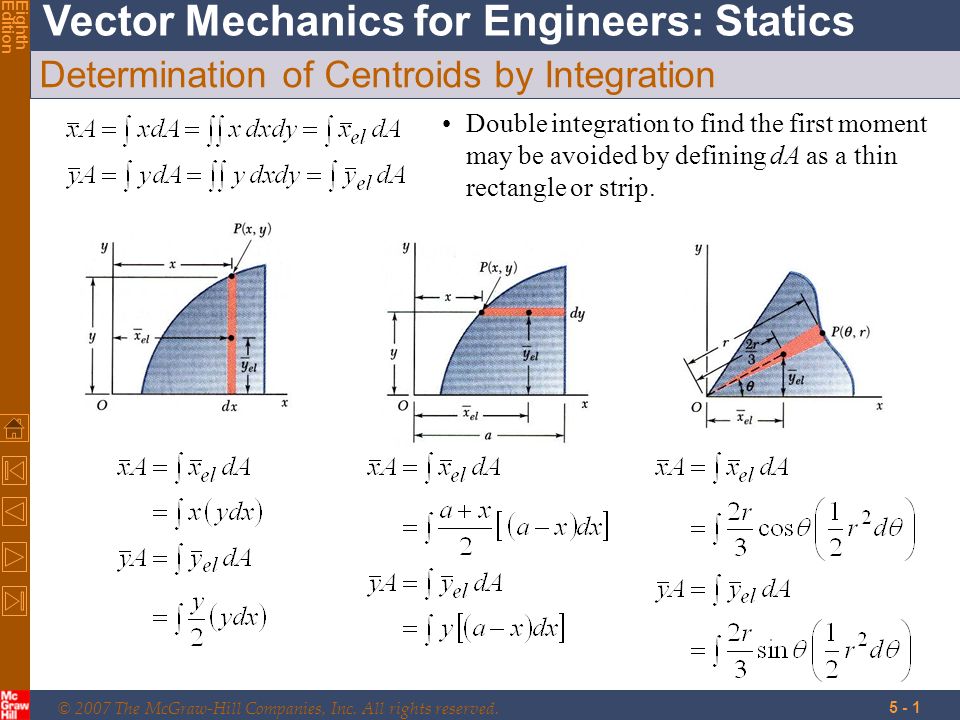
Since the figure is symmetric centroid lies on the x axis Differential element of arc has length dL = rd Total length of arc L = 2 αr xcoordinate of the centroid of differential element x=rcos For a semicircular arc 2α= π centroid lies at 2 r/π L zdL z L ydL y L xdL x ∫ ∫ ∫ = = = L= 2α = 2α =2 =By signing up, you'll get thousands of stepbystepDetermining the centroid of a area using integration involves finding weighted average values x ¯ and , y ¯, by evaluating these three integrals, el el , (772) (772) A = ∫ d A, Q x = ∫ y ¯ el d A Q y = ∫ x ¯ el d A, 🔗 where d A is a differential bit of area called the element A is the total area enclosed by the shape, and is




Find The Centroid Of The Region Bounded By The Line Y X And The Parabola Y X 2 Study Com



Solved 1 How Far From The X Axis Is The Centroid Of The Area Bounded By The Curves X 2 36y The X Axis And The Line X 12 Provide Complete Course Hero
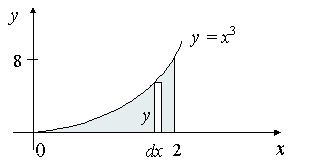
You take moments But first you have to decide which section you are interested in There is a branch between x=10 to \sqrt{} and another between x y = 16 x^2 find centroid bounded by x axis Homework Equations x = (1/A) ∫ x(f(x)) dx and (1/A) (1/2)(f(x))^2 dx = y The Attempt at a Solution I just applied it It is a weird because I would of thought that x would of been at 0 But I didn't get that I x = 9/16 and y = 8/5 Y might be OK but wouldn't x have to be at 0?Centroids Determined by Integration Centroid of area A x ¯ = ∫ a b x c d A A y ¯ = ∫ a b y c d A Centroid of lines L x ¯ = ∫ a b x c d L L y ¯ = ∫ a b y c d L Center of gravity of bodies W x ¯ = ∫ a b x



2




Calculus Ii Lesson 7a Applications Of Integration 6 Centroids Application Center
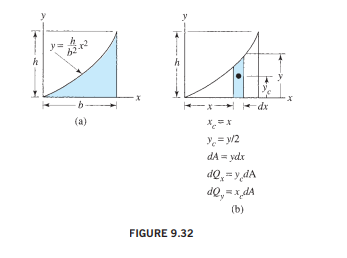
4 y y y y y y y y y y x x = − = − = = = = − = = Therefore, the intersection points are (0, 0) and (4, 2) The centroid of a parabola is found with the equation y = h/b^2 * x^2, where the line y = h Additionally, the area is 4bh/3 The center of mass or centroid of a region is the point in which the region will be perfectly balanced horizontally if suspended from that point So, let's suppose that the plate is the region bounded by the two curves f (x) f ( x) and g(x) g ( x) on the interval a,b a, b So, we want to find the center of mass of the region below



Lesson 12 Centroid Of An Area



1
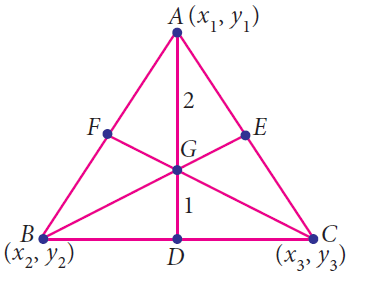
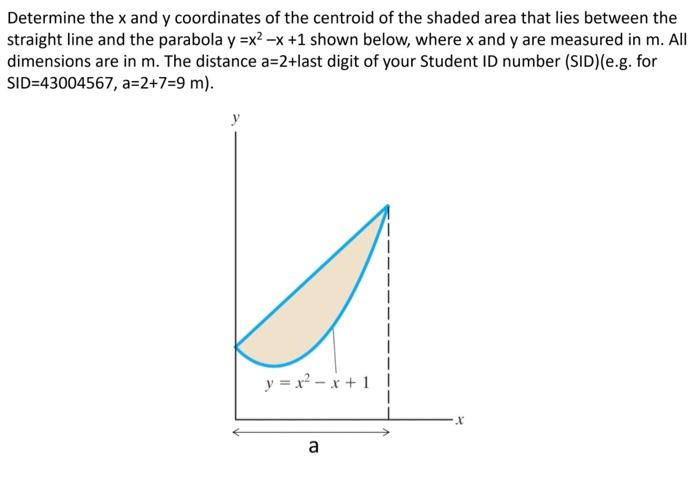
Question Determine the x and y coordinates of the centroid of the shaded area that lies between the straight line and the parabola y =x2 x 1 shown below, where x and y are measured in m All dimensions are in m The distance a=2last digit of your Student ID number (SID) (eg for SID=, a=27=9 m) y = x2x1 aIf the three vertices of the triangle are A(x 1, y 1), B(x 2, y 2), C(x 3, y 3), then the centroid of a triangle can be calculated by taking the average of X and Y coordinate points of all three vertices Therefore, the centroid of a triangle can be written as Centroid of a triangle = ((x 1 x 2 x 3)/3, (y 1 y 2 y 3)/3) Centroid Formula ForCentroids of Lines x z y x z y Exercise 545 Find the Centroid of the wire shown Friday, 1038 AM CE297 FA09 Ch5 Page 4 CE297 FA09 Ch5 Page 5 53 54 Centroids and First Moments of Areas & Lines The first moment of an area with respect to a line of



5 Centroid Of An Area By Integration



Parabolic Segment From Wolfram Mathworld
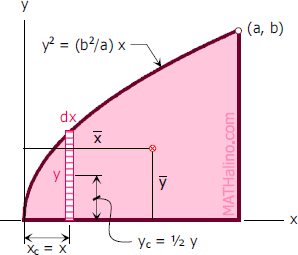
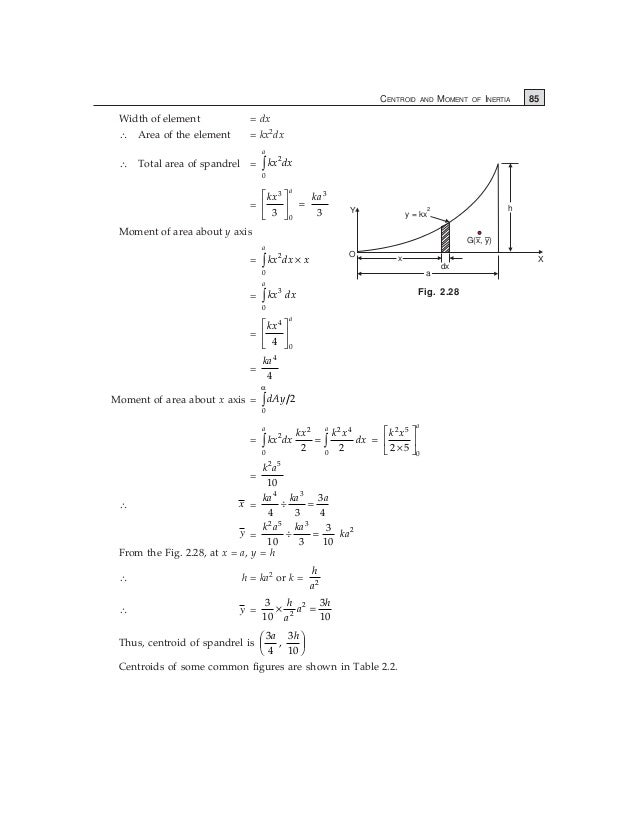
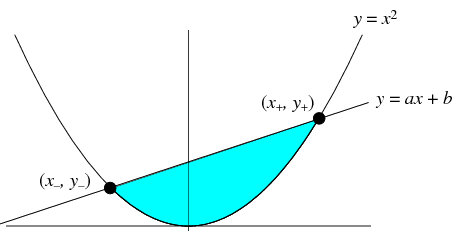
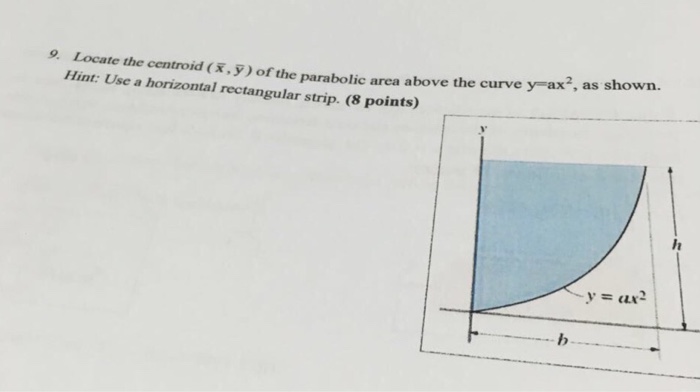
We know that centroid of triangle formed joining fleet of normals drawn from a point always lies on the axis of parabola So, ( h , k ) lies on axis of Parabola y 2 = 4 a x ie = > y = 0 This is not a homework help question, I found a problem when I was doing selfstudy , but I am getting stuck Please tell me if my method is right, or if there are other steps IProblem 705 Determine the centroid of the shaded area shown in Fig P705, which is bounded by the xaxis, the line x = a and the parabola y 2 = kx




Centroid Definition Properties Theorem And Formulas




705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino




Solved Locate The Centroid Of The Shaded Area Bounded By The Locate The 1 Answer Transtutors




Determine The Centroid X Y Of The Shaded Area Youtube




Calculus Ii Lesson 7a Applications Of Integration 6 Centroids Application Center



Solved Find The Centroid Of The Area Bounded By The Parabola 4x X 2 Y And Y 0 Course Hero




Mechanical Engineering Centroids Center Of Gravity 10 Of 35 C G Of A Parabolic Spandrel Youtube



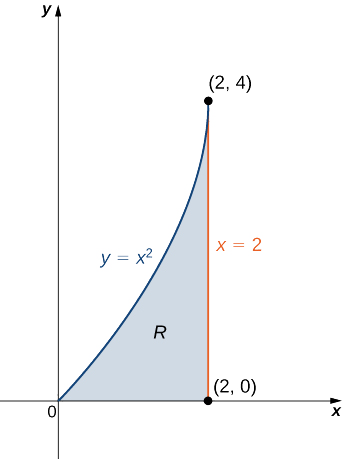
6 6 Moments And Centers Of Mass Calculus Volume 1




Tmmkafzr9wdufm




Solved Locate The Centroid X Bar Of The Parabolic Area Chegg Com
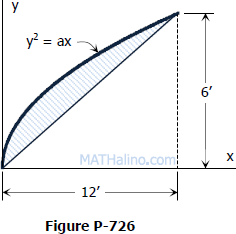



726 Area Enclosed By Parabola And Straigh Line Centroid Of Composite Area Engineering Mechanics Review At Mathalino



Solved A Using Integration Locate The Centroid Of The Area Under The 1 Answer Transtutors



Solved Find The Centroid Of The Area Bounded By The Parabolas X2 Y And Y 9 Course Hero



Given The Region Bounded By The Curve Y X 2 And The Line Y 2x 3 What Is The Area Boded By The Given Region The Moment Of The Region With Respect To X Axis The Moment
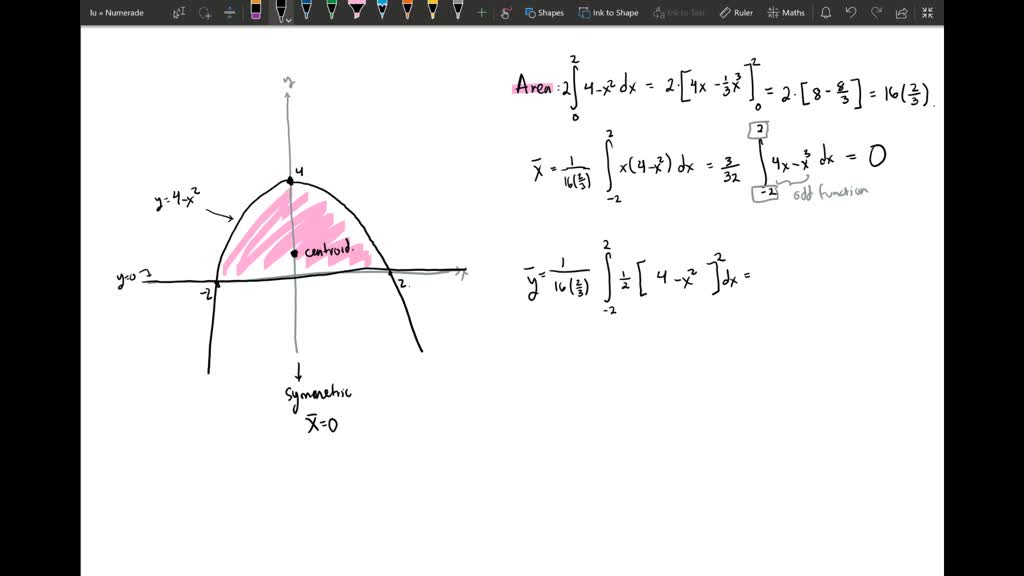



Solved Determine The Coordinates Of The Centroid Of The Area Bounded By The Curve X2 Y A 4 The X Axis And The Y Axis On The First Quadrant




Finding The Centroid Of The Planar Region Bounded By The Parabola Y 4 X 2 And The Line Y X 2 Study Com



K7klmxdgwmnadm




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts




Locate The Centroid Of The Hyperbolic Paraboloid Shown In Fig A Using 1 Single Integration With A Differential Volume Element Parallel To The Xz Plane And 2 Double Integration The Equation Of The




Mechanics Map Centroid Of An Area



Determination Of Centroids By Integration Ppt Video Online Download




Centroid Of Area By Integration Spr18 Youtube




Ch09d Problem 9 7 Locate The Centroid Of The Parabolic Area Solution A H B 2 Da X Dy Xc X 2 Yc Y H A B 0 Y H Dy A H 3 1 Xc B 2 H B 2 0 Xc Course Hero



Find The Exact Coordinates Of The Centroid Mathskey Com



How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic




Find The Centroid Of The Area Bounded By The Parabola Y 4 X 2 And The X Axis Study Com




Find The Centroid Of The Region Bounded By Y X Z Y X Homeworklib



Solved Determine The Centroids For The Parabolic Spandrel Shown In Fig 1 Answer Transtutors



2




Find The Centroid Of The Region Bounded By The Parabolas Y X 2 4 And Y 0 75x 2 3 Study Com




Find The Centroid Of The Region Bounded By The Parabola Y X 2 The Line X 2 And The X Axis Study Com




Engineering Mechanics Statics Ppt Download




List Of Centroids Wikipedia
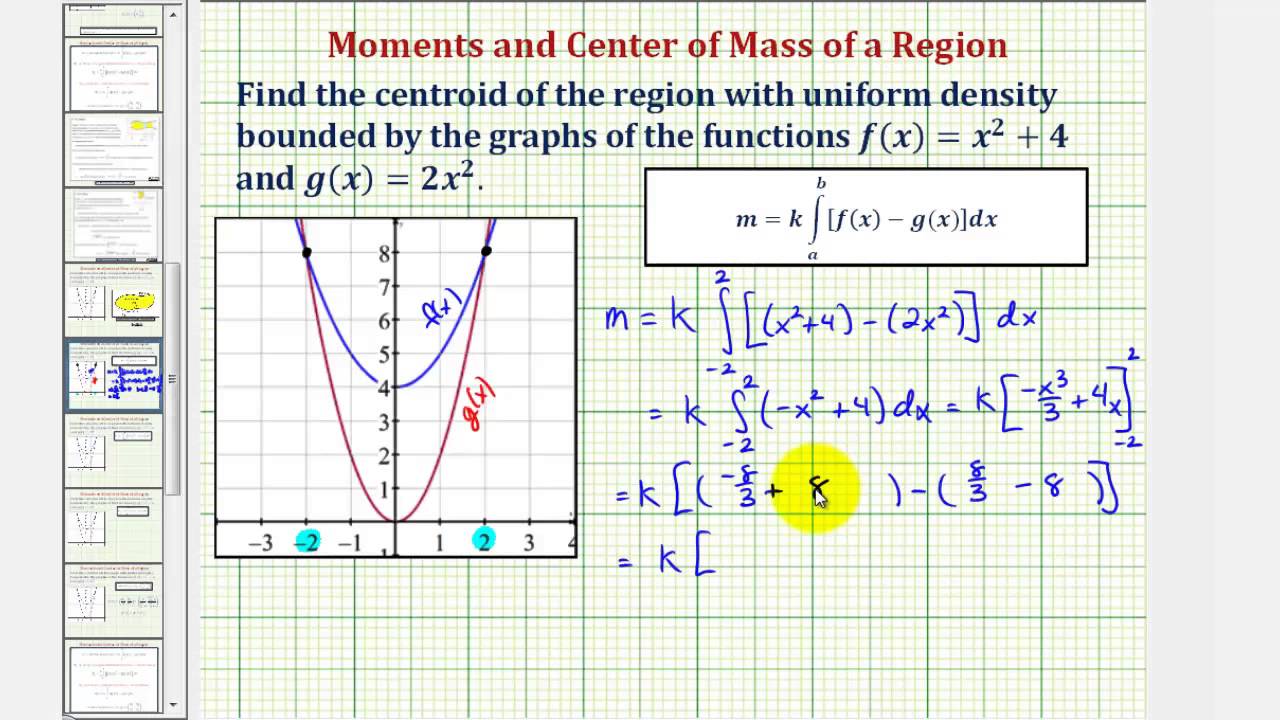



New Version Available Find The Centroid Of A Bounded Region Involving Two Quadratic Functions Youtube




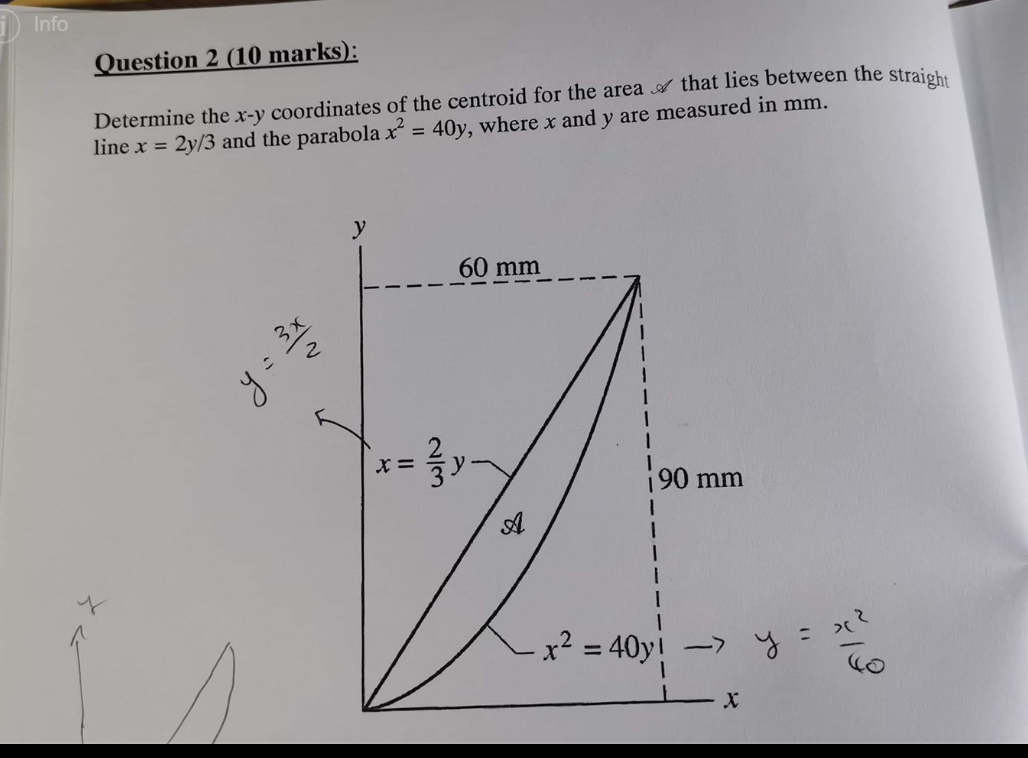
Determine The Coordinates Of The Centroid Of The Area That Lies Between The Straight Line X 2y 3 And The Parabola X 2 40y Where X And Y Are Measured In Mm See Fig A



2



2
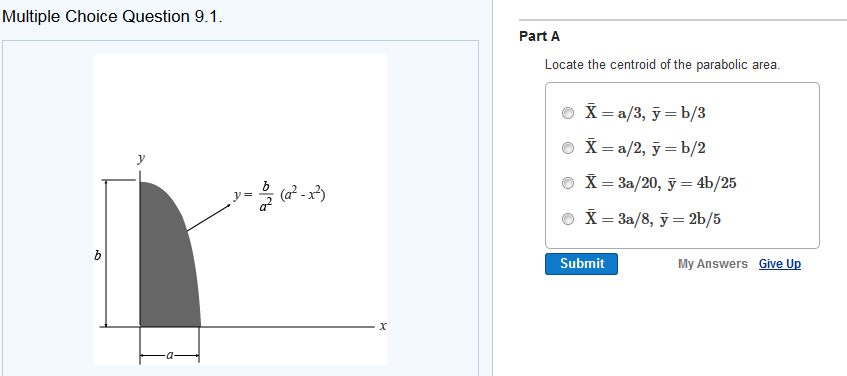



Solved Locate The Centroid Of The Parabolic Area Chegg Com
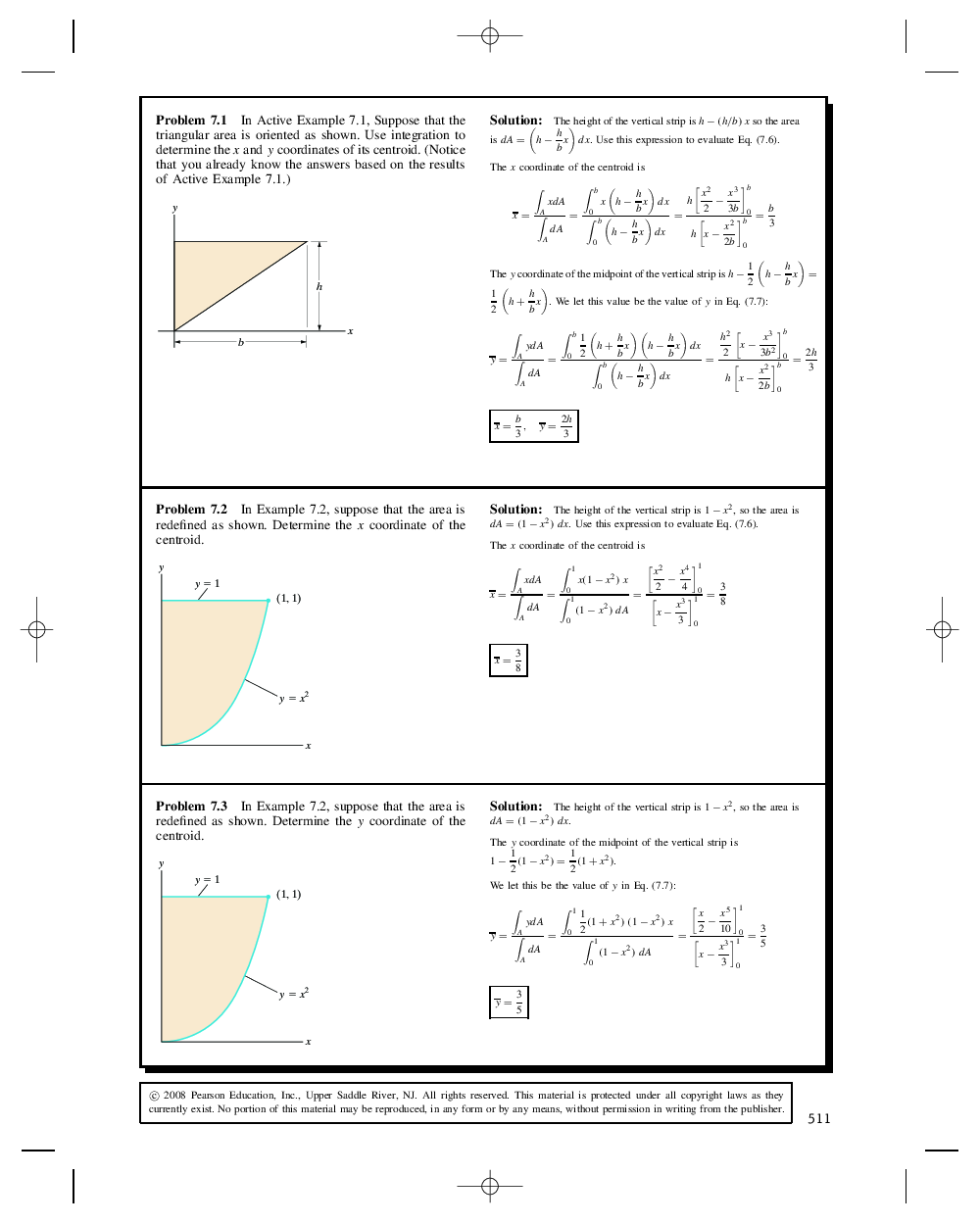



Statics Bedford Chap 07 Pdf Docer Com Ar




8 Further Applications Of Integration Further Applications Of



Area By Integration Mathalino Reviewers ged With Area By Integration
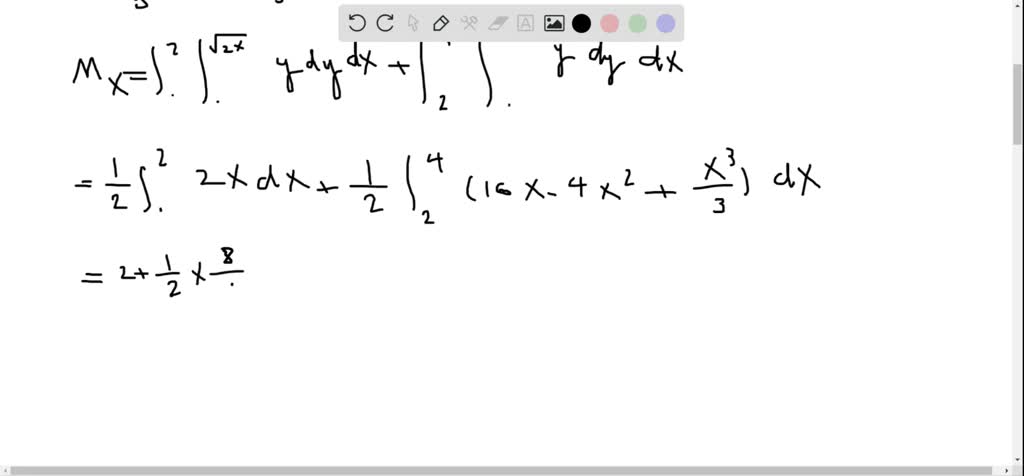



Solved Find The Ordinate Of The Centroid Of The Region Between The Parabola Y 1 Aˆ X2 And The Line Y 1 Aˆ X
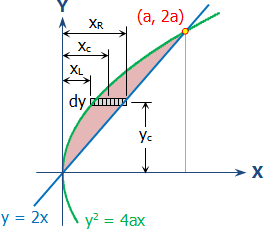



Centroid Of Area Bounded By Parabola And Line At Integral Calculus Forum Mathalino



15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts
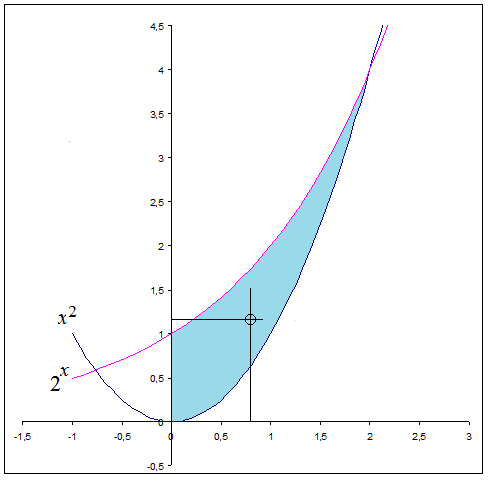



Find Centroid Of Region Of Two Curves Mathematics Stack Exchange



Solved Locate The Centroid X Y Of The Parabolic Area Chegg Com



What Is The Centroid Of The Solid Formed By Revolving The Region Bounded By Y 4 X 2 And Y X And X 0 About Y Axis Quora



Solved Info Question 2 10 Marks Determine The X Y Chegg Com



Solved Whatever The Value Of P 0 In The Equation Y Chegg Com



8 Further Applications Of Integration Further Applications Of
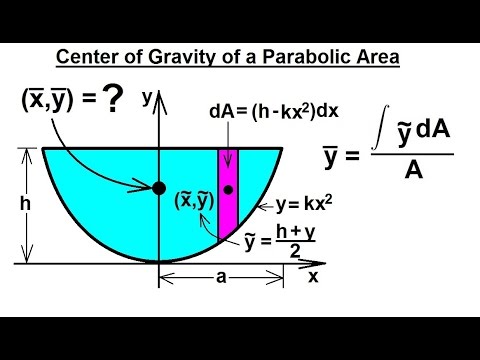



Mechanical Engineering Centroids Center Of Gravity 9 Of 35 C G Of A Parabolic Area Youtube



2
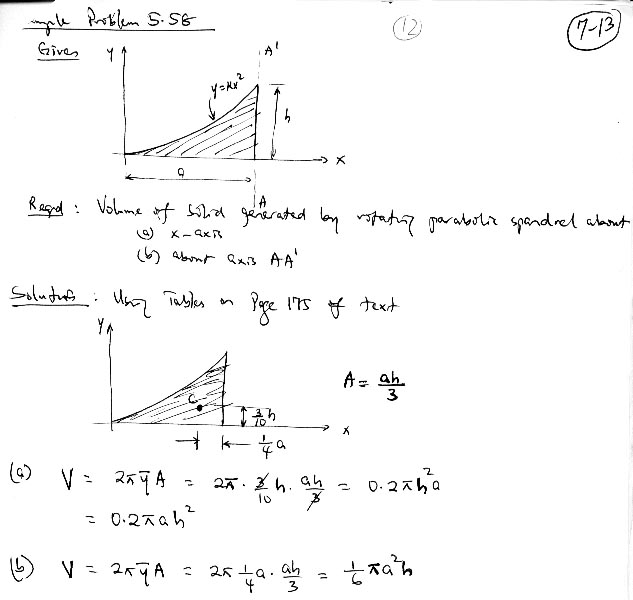



Centroids Centre Of Mass Centres Of Gravity
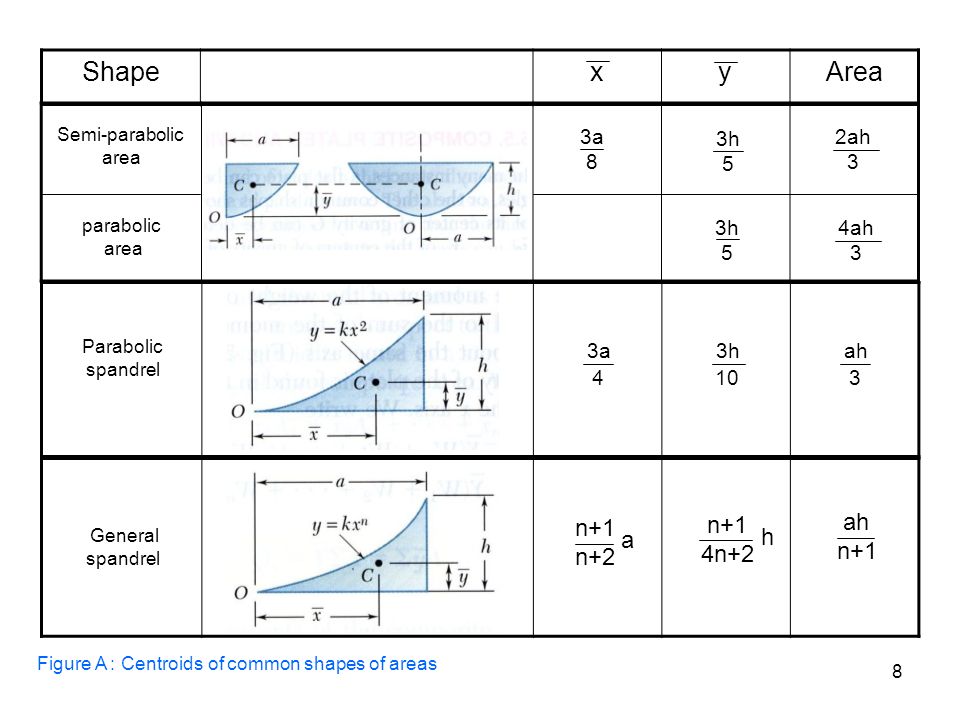



Centroids And Centers Of Gravity Ppt Video Online Download
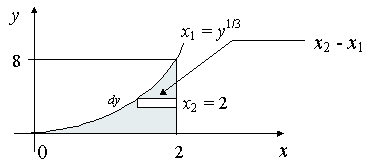



5 Centroid Of An Area By Integration




List Of Centroids Wikipedia
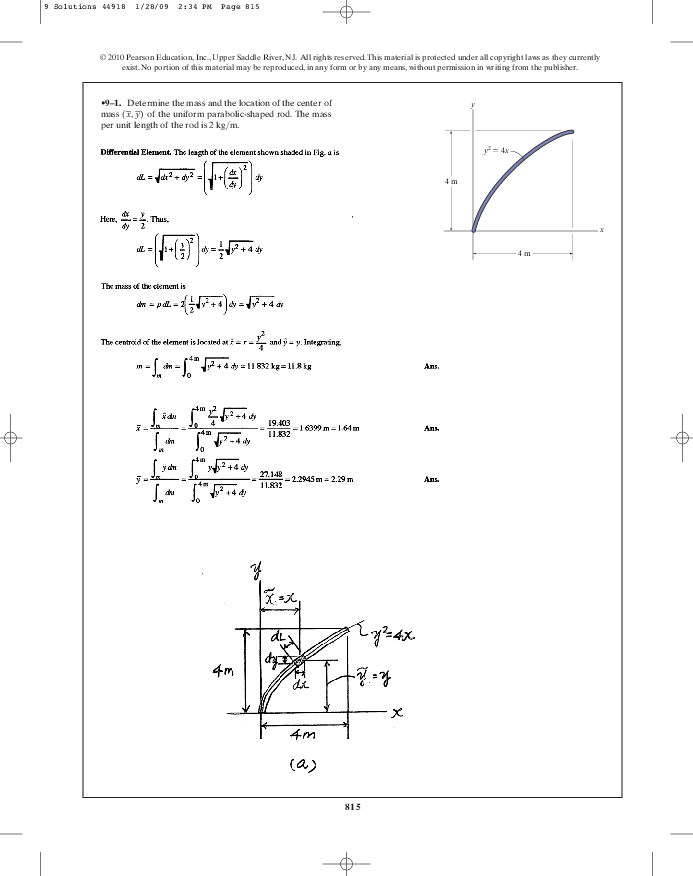



Pdf Chapter 9 Rafey Imtiaz Academia Edu
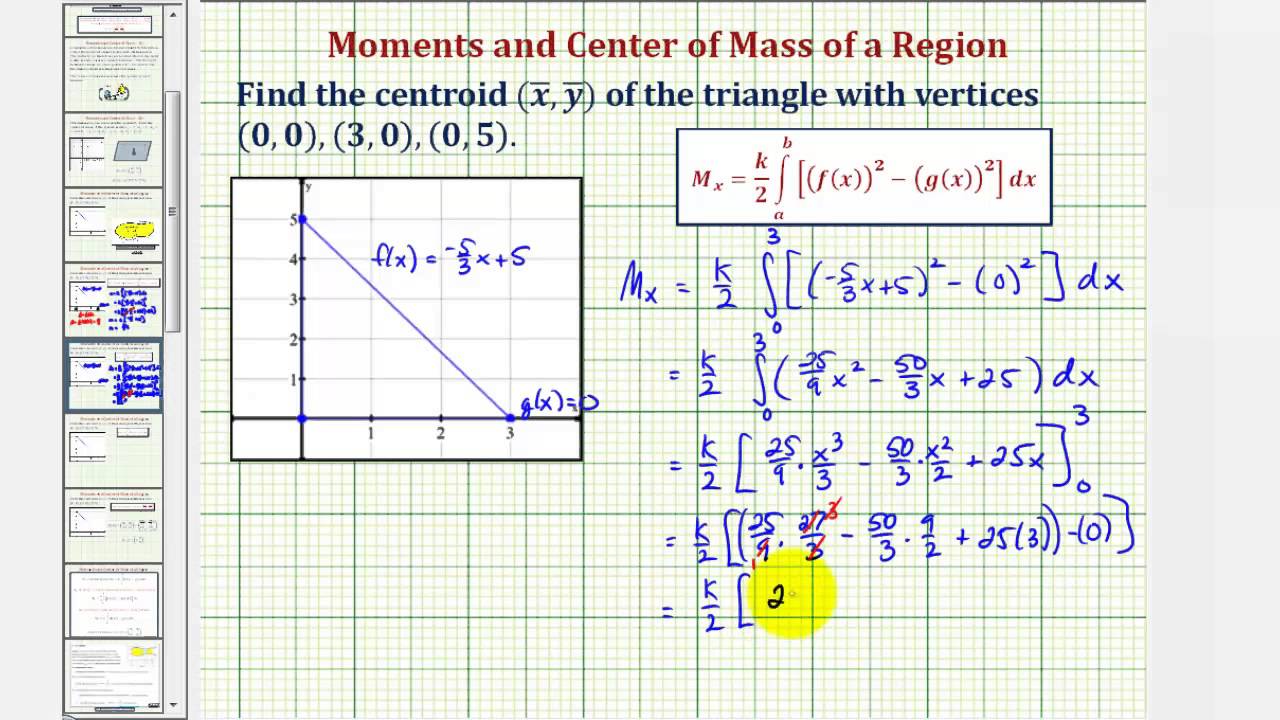



Calculate The Centroid Or Center Of Mass Of A Region Video Lessons Examples Step By Step Solutions




Solved X 2 A Y B Y Chegg Com



2




Locate The Centroid X Bar Of The Parabolic Area Enclosed By The Curve Y H X 2 A 2 The Line X A And Y H Take A 8 In And H 10 In Study Com
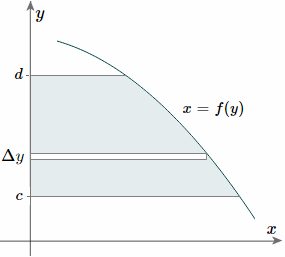



5 Centroid Of An Area By Integration
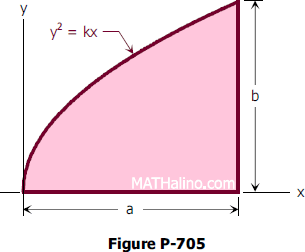



705 Centroid Of Parabolic Segment By Integration Engineering Mechanics Review At Mathalino
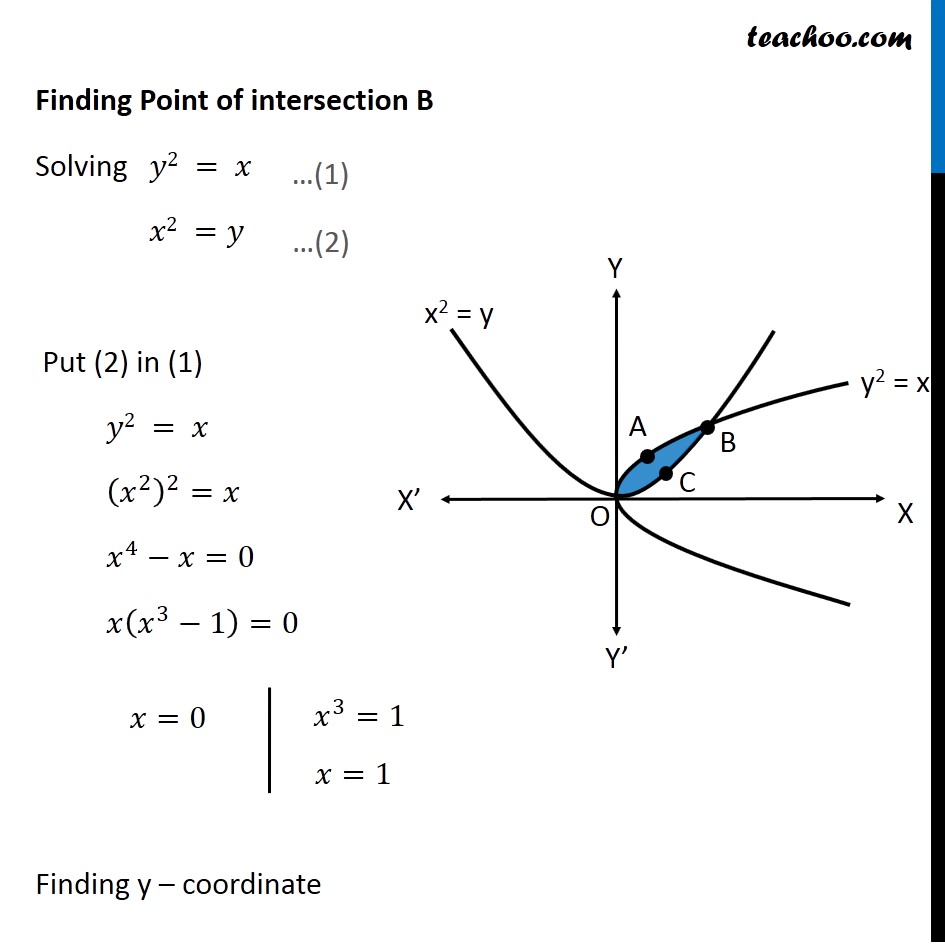



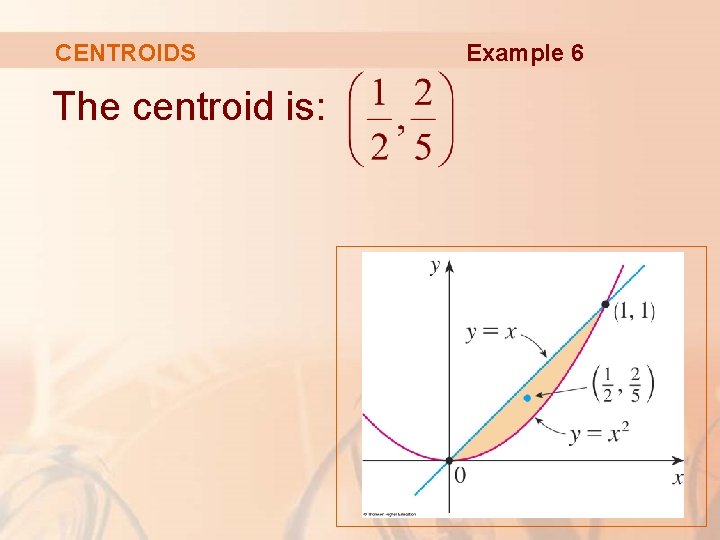
Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X
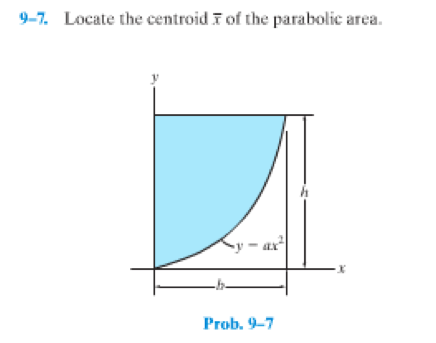



Solved Locate The Centroid X Of The Parabolic Area Chegg Com




Centroid Area Moments Of Inertia Polar Moments Of Inertia Radius Of Gyration Of A Parabolic Spandrel Sub Parabolic Area




Mechanical Engineering Centroids Center Of Gravity 11 Of 35 C G Of A General Spandrel 1 Youtube



5 Centroid Of An Area By Integration




List Of Centroids Wikipedia




Calculus Ii Center Of Mass
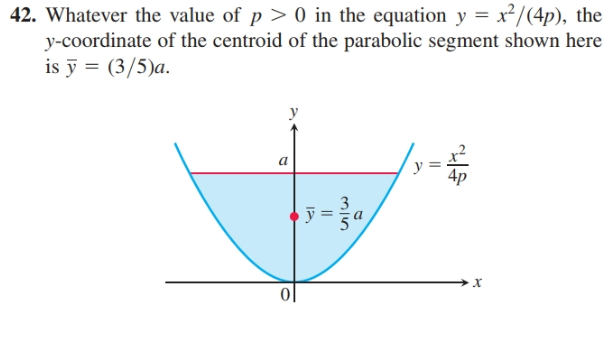



Answered 42 Whatever The Value Of P 0 In The Bartleby




Centroids Reference Table Calcresource




Centroid Area Moments Of Inertia Polar Moments Of Inertia Radius Of Gyration For The First Quadrant Of A Parabolic Area




Find The Centroid Of The Area Of Of A Plane Region With Sides Given By X 2 Y 2 4 Mathematics Stack Exchange




Centroid Of Volume Bounded By A Line And A Parabola Mathematics Stack Exchange
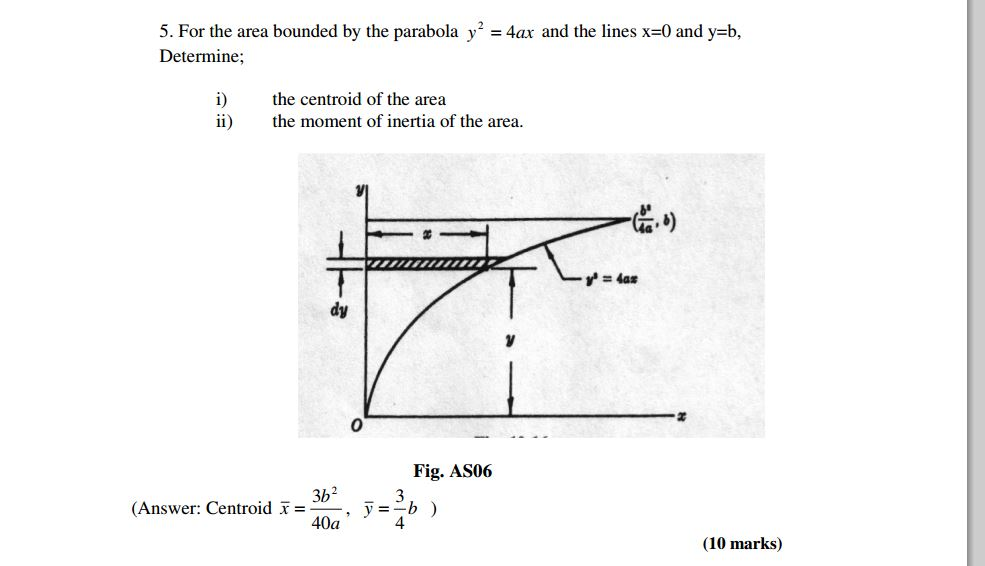



Solved 5 For The Area Bounded By The Parabola Y 2 4ax And Chegg Com



1
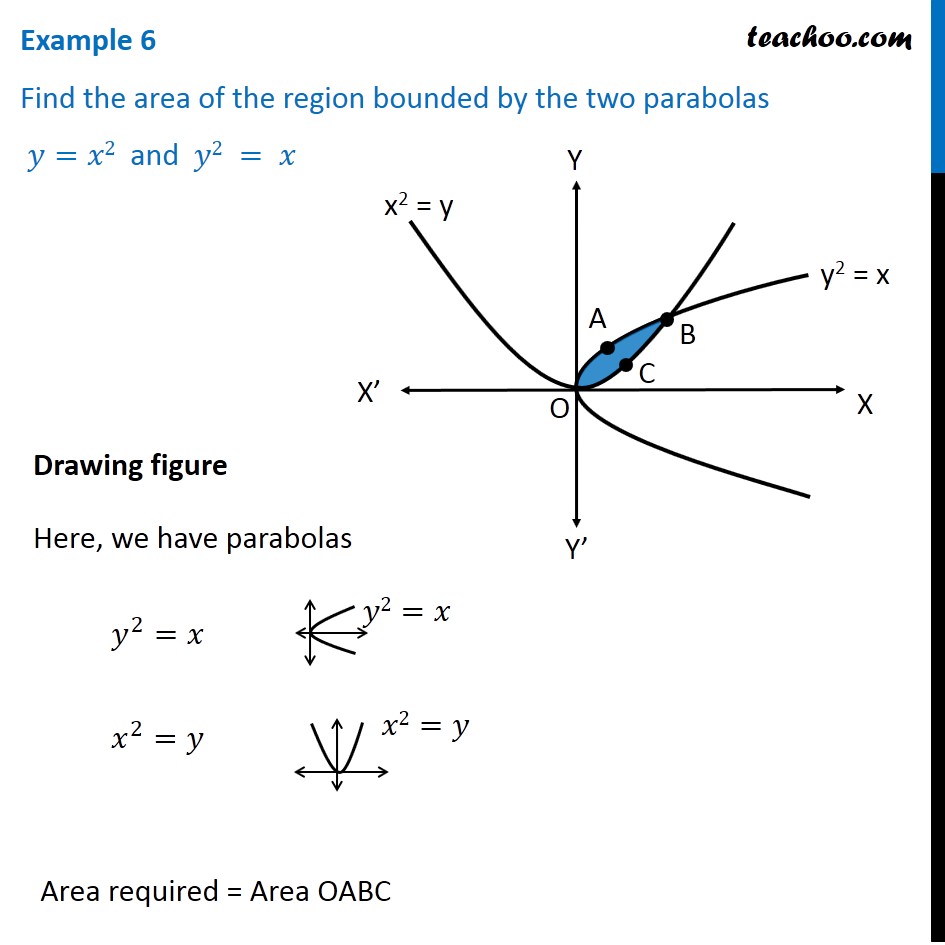



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X



0 件のコメント:
コメントを投稿